Inleiding

Problemen, algoritmen en oplossingen vormen een drieëenheid in de informatica. Elke vraag die men in één of andere taal kan stellen is een probleem, maar zo’n probleem is voor de informaticus niet noodzakelijk interessant. Een probleem wordt pas interessant voor de informaticus als er sprake is van een—doorgaans oneindige—verzameling van soortgelijke vragen die op dezelfde manier naar een oplossing gebracht kunnen worden. In zo’n geval is deze verzameling van problemen te vangen met eenzelfde methode, en we spreken dan al snel van een algoritme om het probleem op te lossen [Lee09]. Je kan een algoritme zien als een programma. Het verschil is dat een programma meestal expliciet in één of andere programmeertaal zegt wat een programma moet doen, terwijl een algoritme een veel globalere beschrijving is van de stappen die moeten worden uitgevoerd. De stappen die moeten doorlopen worden kunnen we in een flowchart visualiseren. Er bestaan verschillende soorten algoritmen, namelijk sorteeralgoritmen, numerieke algoritmen, grafenalgoritmen. In dit artikel wordt Dijkstra’s Kortstepad-algoritme – ook bekend als Dijkstra’s algoritme – besproken.

Kortstepad-algoritme

Dijkstra’s algoritme is een graafalgoritme. Het probleem is het vinden van het kortste pad in een gewogen graaf tussen twee punten. Een gewogen graaf is een verzameling van knopen waarin elke knoop is opgeno- men met een respectievelijk gewicht. Dit algoritme is een klassieker. Het is ruim 50 jaar gelden in 1959 gepubliceerd door de Nederlandse informaticus Edsger Dijkstra.

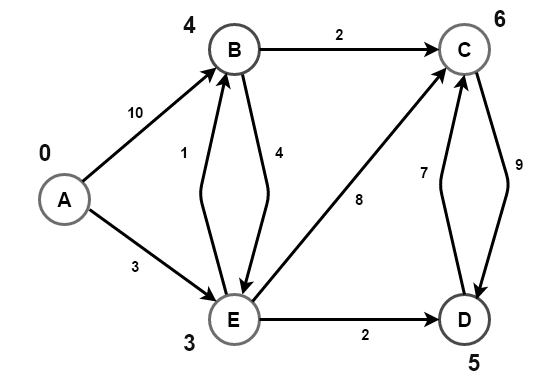
Gegeven is een graaf G = (V, E) met E ⊆ V × V , een gewichtsfunctie f : E → R+ (alleen positieve gewichten) en een speciaal startpunt S in de graaf, en gevraagd is voor elk punt A in de graaf de lengte van een pad van S naar A te vinden zo dat de som van de gewichten van de kanten in dat pad minimaal is.

Gebruik van het algoritme

Routeplanners

Het algoritme wordt vaak gebruikt in routeplanners. Wanneer je van stad A naar stad B wil genavigeerd worden, verwacht je natuurlijk de kortste of meest tijdsefficiente route. Een expresweg zal een ander gewicht hebben dan een buurtweg.

Sociale netwerk-applicaties

In vele socialmedia-applicaties heb je wel al eens een suggestie gekregen om mogelijkse mensen die je kent als nieuwe vriend toe te voegen of zie je bepaalde content waar je mogelijks in geïnteresseerd bent. Om deze berekeningen te maken, wordt vaak het kortste pad-algoritme gebruikt. [Gee]

IP routing

Open Shortest Path First (OSPF) is een routingprotocol waarbij het beste pad tussen twee sources en de bestemmmingsrouter berekend wordt. Hiervoor wordt Dijkstra’s algoritme gebruikt. [K H17]

Werking van het algoritme

De aanpak die Dijkstra koos is de volgende: aan het begin van de algoritme is er precies één knoop waarvan we met zekerheid kunnen zeggen wat de afstand tot S is, namelijk S zelf. Omdat alle afstanden in de graaf groter dan 0 zijn, kunnen we geen korter pad naar S vinden dan het pad zonder kanten. De afstand van S tot S is dus met zekerheid 0. Dit wetende, kunnen we van één andere knoop de afstand tot S bepalen. S heeft namelijk een aantal buren v 1 , v 2 , . . . , v k die allemaal door een kant met gewicht groter dan 0 met S verbonden zijn. Elk pad naar een willekeurige knoop in de graaf (dus zeker naar v 1 , . . . , v k gaat door één van deze knopen. Als dus v m een buur van S is waarvan het gewicht van de verbindende kant minimaal is, dan kan er geen pad in de graaf zijn dat korter is dan het gewicht van deze kant. Kortom v m vormt samen met S een groep knopen waarvan we de afstand tot S in de graaf weten. Noem deze groep knopen W . De algoritme breidt nu stap voor stap de verzameling W uit, totdat alle knopen in de graaf in W zitten.

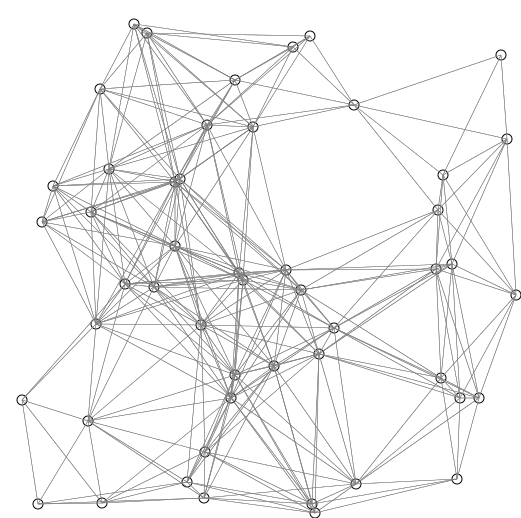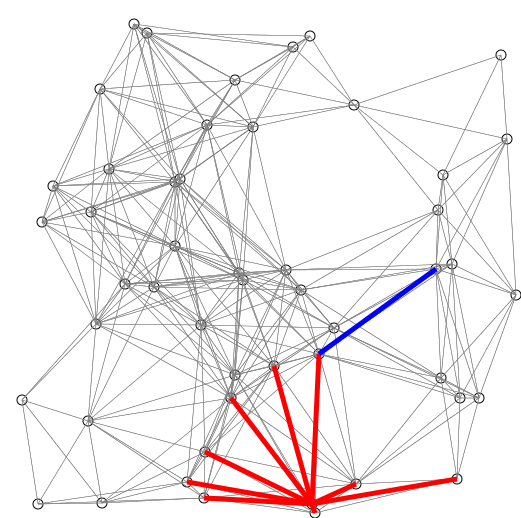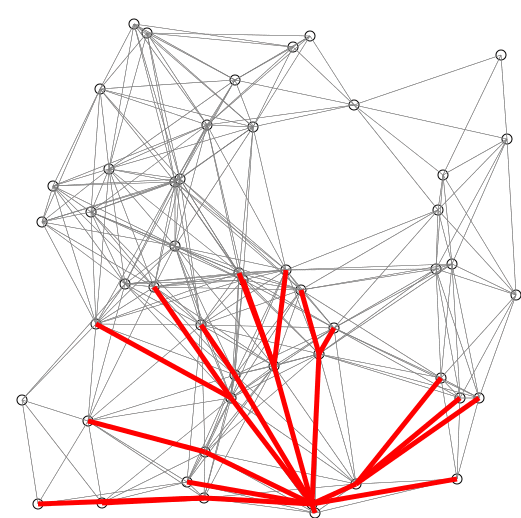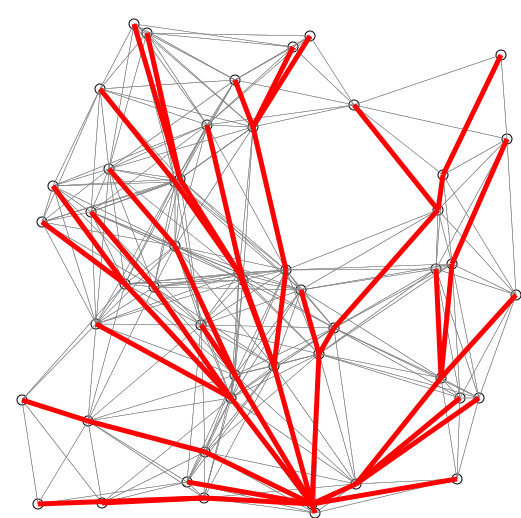
Op elk moment geldt dat we, kijkend naar de buren van knopen in W , zien dat we één van deze knopen ook het kortste pad in de graaf weten. Dat is namelijk van de knoop, v, waarvan de afstand tot S, uitsluitend via knopen in W , minimaal is. Immers, als het korste pad van S naar v niet uitsluitend via knopen in W zou lopen, dan zou het via een andere knoop v buiten W lopen. Laat v zonder beperking van algemeenheid de eerste knoop zijn die op het korste pad naar v ligt en niet in W zit. Dan loopt het pad van S naar w uitsluitend door knopen in W , en is korter dan het pad dat uitsluitend door knopen in W naar v loopt, want v 6 = w. Dat is in tegenspraak met de manier waarop v gekozen is. [Dij59]

Java-implementatie


	import java.util.*;

	// Data structure to store graph edges
	class Edge {
		int source, dest, weight;

		public Edge(int source, int dest, int weight) {
			this.source = source;
			this.dest = dest;
			this.weight = weight;
		}
	}

	// Data structure to store heap nodes
	class Node {
		int vertex, weight;

		public Node(int vertex, int weight) {
			this.vertex = vertex;
			this.weight = weight;
		}
	}

	// class to represent a graph object
	class Graph {
		// A List of Lists to represent an adjacency list
		List<List<Edge>> adjList = null;

		// Constructor
		Graph(List<Edge> edges, int N) {
			adjList = new ArrayList<>();

			for (int i = 0; i < N; i++) {
				adjList.add(new ArrayList<>());
			}

			// add edges to the undirected graph
			for (Edge edge: edges) {
				adjList.get(edge.source).add(edge);
			}
		}
	}

	class Main {
		private static void getRoute(int[] prev, int i, List<Integer> route) {
			if (i >= 0) {
				getRoute(prev, prev[i], route);
				route.add(i);
			}
		}

		// Run Dijkstra's algorithm on given graph
		public static void shortestPath(Graph graph, int source, int N) {
			// create min heap and push source node having distance 0
			PriorityQueue<Node> minHeap = new PriorityQueue<>(Comparator.comparingInt(node -> node.weight));
			minHeap.add(new Node(source, 0));

			// set infinite distance from source to v initially
			List<Integer> dist = new ArrayList<>(Collections.nCopies(N, Integer.MAX_VALUE));

			// distance from source to itself is zero
			dist.set(source, 0);

			// boolean array to track vertices for which minimum
			// cost is already found
			boolean[] done = new boolean[N];
			done[source] = true;

			// stores predecessor of a vertex (to print path)
			int[] prev = new int[N];
			prev[source] = -1;

			List<Integer> route = new ArrayList<>();

			// run till minHeap is empty
			while (!minHeap.isEmpty()) {
				// Remove and return best vertex
				Node node = minHeap.poll();

				// get vertex number
				int u = node.vertex;

				// do for each neighbor v of u
				for (Edge edge: graph.adjList.get(u)) {
					int v = edge.dest;
					int weight = edge.weight;

					// Relaxation step
					if (!done[v] && (dist.get(u) + weight) < dist.get(v)) {
						dist.set(v, dist.get(u) + weight);
						prev[v] = u;
						minHeap.add(new Node(v, dist.get(v)));
					}
				}

				// marked vertex u as done so it will not get picked up again
				done[u] = true;
			}

			for (int i = 1; i < N; ++i) {
				if (i != source && dist.get(i) != Integer.MAX_VALUE) {
					getRoute(prev, i, route);
					System.out.printf("Path (%d -> %d): Minimum Cost = %d and Route is %s\n", source, i, dist.get(i), route);
					route.clear();
				}
			}
		}
	}

Complexiteit

Een algoritme is een duidelijk gespecificeerde verzameling instructies die de computer zal volgen bij het op- lossen van een probleem. Wanneer een algoritme voor een bepaald probleem opgesteld en correct bevonden is, dan bestaat de volgende stap in het bepalen van de hoeveelheid resources, zoals uitvoeringstijd en ge- heugenruimte, die het algoritme zal vereisen. Deze stap wordt de analyse van een algoritme genoemd. [Fac14]

Het belangrijkste aspect van een programma is meestal zijn uitvoeringstijd. Echter, het volstaat niet om alleen aan de uitvoeringstijd aandacht te besteden. Men moet ook rekening houden met andere factoren, zoals de ruimte nodig om het programma uit te voeren. Een analyse zal gebruikelijk bestaan uit het inschatten van de nodige uitvoeringstijd voor een algoritme en het inschatten van de benodigde geheugenruimte voor een datastructuur.

Big O-Notatie

Een bovengrens voor de uitvoeringstijd van het algoritme geeft aan wat de hoogste orde van toename is die een algoritme kan hebben. Merk op dat de bovengrens niet hetzelfde is als de slechtst mogelijke uitvoe- ringstijd voor een gegeven input van grootte n. Het is eerder een bovengrens voor de orde van toename, uitgedrukt in een vergelijking.

Voor de zinsnede “heeft een bovengrens voor zijn orde van toename f (n)” is een speciale notatie ingevoerd, de zogenaamde O-notatie. Wanneer de orde van toename van een algoritme (bv. in het slechtste geval) een bovengrens g(n) heeft, dan zegt men dat dit algoritme “behoort tot de verzameling O(g(n))”. Bijvoorbeeld, wanneer n 2 even snel toeneemt als de uitvoeringstijd T (n) van het algoritme in het slechtste geval, dan zeggen we dat het algoritme behoort tot O(n 2 ). We noteren dit als T (n) = O(n 2 ).

Complexiteit van Single-Source Shortest Paths

Wanneer we de tijdscomplexiteit van Dijkstra’s algoritme willen berekenen, moeten in het achterhoofd houden op welke manier we dit geïmplementeerd hebben. Als we dit doen op de “basis”manier zoals Dijkstra het zelf beschreef is dit algoritme O(V 2). Natuurlijk zijn programmeertalen geëvolueerd en bestaat er nu een datastructuur als een Binary Heap. Wanneer we het algoritme implementeren met een binary heap, is de complexiteit O((E + V )logV ). Als laatste kan er ook nog gebruik gemaakt worden van een Fibonacci Heap waardoor het algoritme nog optimaler is en de complexiteit dan maar O(E + V logV ) is.

Referenties